Lecture 2

1/27/25 - Gödel’s Incompleteness Theorems §

Limitations of Math and Reasoning

• Can you reason about anything
• Take faith and trust things
• The apple is red
  • We both argue what “apple” and “red” is
• Both consider what is real - Gödel
• Statements that are true but cannot be proven
• Concerning - limitations in math
• You, I, and a computer can reason about it
  • A computer has limitations in reasoning
• Finite number of atoms
• We want to see how things are limited

Real world vs Abstract world

1. Observation (Real world)
2. Hypothesis (Abstract world)
3. Test (Real world) Back and forth between real and abstract

Peano’s Axioms

1. Symbol ”$0$”
2. $S(a)$: If $a$ exists in $\mathbb{N}$, then $a+1$ exists in $\mathbb{N}$
3. $0$: $0$ is not a successor of anything. $\nexists a\in \mathbb{N},S(a)=0$
4. If for any $x,y\in \mathbb{N}$, $S(x)=S(y)$, then $x=y$
5. Induction Axiom: If $0\in S,\forall x\in S,S(x)\in S,$ then $S=\mathbb{N}$

$\aleph =(\mathbb{N},+,\times )$ $S^i(x)=S(S(S(x)))$ $x+i=S^i(x)$

Gödel’s Incompleteness Theorems $⊢x:$ $x$ is a theorem in the math symbol (e.g. $\aleph$ is a mathematical symbol)

1. $\exists$ a sentence $C\in \aleph$, such that $/⊢C$ and $/⊢\neg C$. ($C$ is not a theorem, and not $C$ is not a theorem).
   1. “There is a truth which cannot be derived”
2. Assume $\aleph$ is a consistent (if you could derive a theorem, the complement could also be derived). Then $\aleph /⊢\text{const}(\aleph )$
   1. “There are things in $\aleph$ that cannot be derived by $\aleph$” Mathematics is a tool, but it has limitations

• There is a limit to how far the telescope can see.

Proof (using diagonalization): Liar’s paradox

• High level: look at all sentences involving one variable
  • Show that the proof is itself, which can’t be derived

Gödel Numbering - $g:$ Theorem, Proofs $\to \mathbb{N}$ $2\in \mathbb{N}\leftarrow$ we can replace this with a sequence of numbers $\in ,\forall ,\exists ,=,\ne ,>,<$

Symbol	Gödel Number
$\in$	1
2	24
$\mathbb{N}$	101

$2\in \mathbb{N}:24,1,101=2^{24}\cdot 3^1\cdot 5^{101}$ - unique mapping

• Capture a proposition with a number
• Proof using 1 number

Claim: Given $n\in \mathbb{N}$, if $g(x)=n$, $x$ is known to be a symbol/theorem/proof, then $x$ can be computed from $n$

Proof: $n={\prod }_{i=[k]}{p}_i^{a_i}\cdots$ for some $k\in \mathbb{N}$ and $a_1,\dots ,a_k\in \mathbb{N}$

$p_1<p_2<\cdots <p_k$, $p_i$ is the $i$-th prime in increasing order.

True for $n-1$ symbols Functional programming

• Need to show that there are not two different encodings

$\text{Proof}(x,y)$ is true if $y$ is proved by proof $x$ $\text{Pr}(y):=\exists x,\text{Proof}(x,y)$, $y$ is a theorem Lemma:

1. If $⊢y$ then $⊢\text{Pr}(y)$ - collection of statements which can be proven
2. $⊢\text{Pr}(x⟹y)⟹(\text{Pr}(x)⟹\text{Pr}(y))$
3. $⊢Pr(y)⟹\text{Pr}(\text{Pr}(y))$ - If it is possible to derive the proof of $y$, then the proof of $y$ has a proof

Not tested $B_1(n),B_2(n),\dots ,B_i(n),\dots$ - all possible statements with one variable

Consider: $⊢\text{Pr}(B_n(n))$

• There does not exist a proof that $B_n(n)$ is true
• $\exists$ fixed $k\in \mathbb{N},B_k(n)=\neg \text{Pr}(B_n(n))$
• $⊢B_k(n)⟺\neg \text{Pr}(B_n(n))$

$⊢\forall n\in \mathbb{N},(B_k(n)⟺\neg \text{Pr}(B_n(n)))$

$n=k$ $⊢B_k(k)⟺\neg \text{Pr}(B_k(k))$ $B_k(k)$ is a theorem if and only if there does not exist a proof of $B_k(k)$

Lemma: Let $A(x)$ be some arbitrary property in some math system with one variable. Then $\exists$ sentence $D$: $⊢D⟺A(g(D))$ - it’s Gödel numbering is a property

Turing’s most famous work - showing what can’t be done

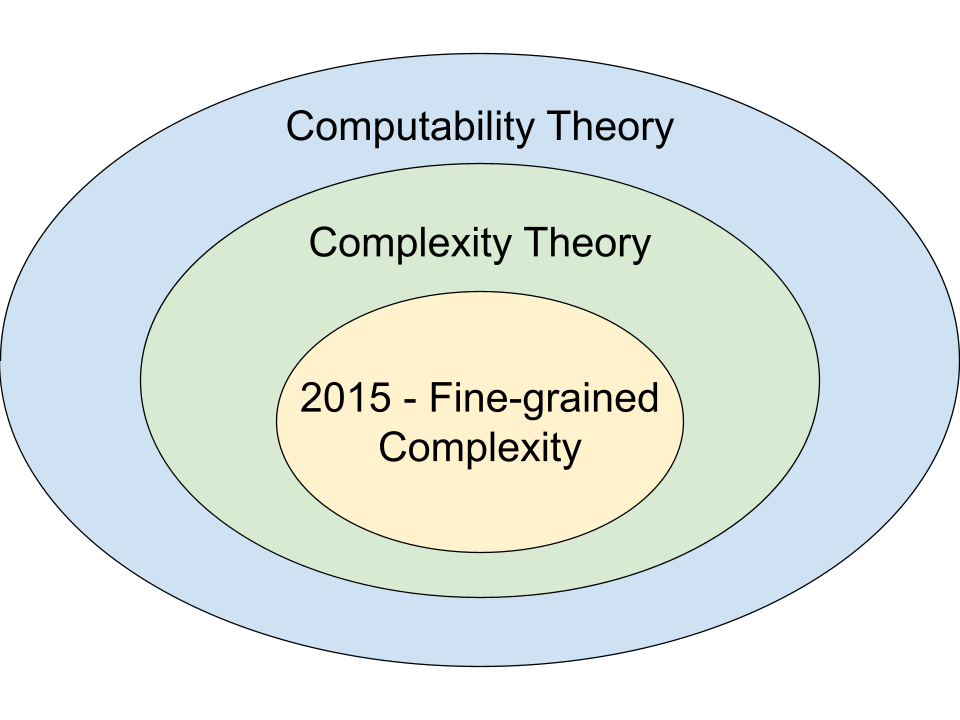
• After computability theory - then what can be done quickly?
• Fine-grained complexity - problems in $P$ that you can’t do quickly